여러 소프트웨어 테스트의 단골 문제인 DP에 대해 간략하게 정리합니다.
위키 백과의 DP에 대한 정의는 다음과 같습니다.
동적 계획법의 원리는 매우 간단하다. 일반적으로 주어진 문제를 풀기 위해서, 문제를 여러 개의 하위 문제(subproblem)로 나누어 푼 다음, 그것을 결합하여 최종적인 목적에 도달하는 것이다. 각 하위 문제의 해결을 계산한 뒤, 그 해결책을 저장하여 후에 같은 하위 문제가 나왔을 경우 그것을 간단하게 해결할 수 있다. 이러한 방법으로 동적 계획법은 계산 횟수를 줄일 수 있다. 특히 이 방법은 하위 문제의 수가 기하급수적으로 증가할 때 유용하다.
복잡한 정의 때문에 처음 들었을 때 이해가 잘 되지 않는 분들을 위해 신입 스터디 때 사용했던 예를 통해 설명드립니다.
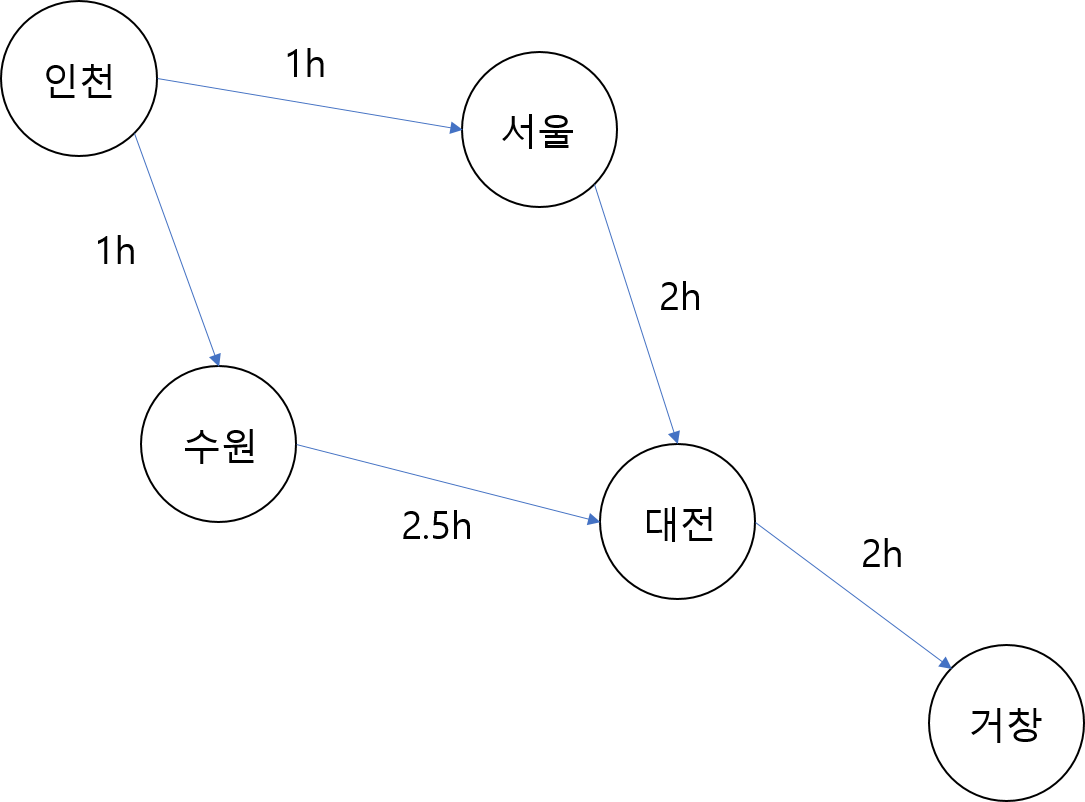
인천에서 거창까지 가는 최소 시간을 출력하는 문제가 주어졌다고 가정합시다. 이를 해결하는 대략적인 수도 코드는 다음과 같습니다. (이해를 돕기 위해 인덱스가 아닌 지역명으로 대체합니다.)
//arr은 노드의 개수 만큼 resize 시켜준 뒤,
//arr[i].push_back(make_pair(j,cost));의 형태로 삽입한다.
vector < vector < pair < int,int > > > arr;
int solution(int pos){
if(pos=="거창") return 0;
int ret=INF;
for(int i=0;i<arr[pos].size();i++){
int there = arr[pos][i].first;
int cost = arr[pos][i].second;
ret=min(ret,solution(there)+cost);
}
return ret;
}
int main(){
printf("%d\n",solution("인천"));
}
그러나 이와 같은 단순 재귀형 코드는 연산을 반복한다는 단점은 가집니다. 예를 들어 인천을 호출된 재귀 함수는 인천과 직접 연결되는 모든 지역을 탐색합니다. 서울을 먼저 연산한다 가정하면 인천에서 서울까지 1시간, 서울에서 대전까지 2시간, 대전에서 거창까지 2시간이 걸림을 문제에서 주어진 일정한 계산 과정을 통해 도출해 냅니다.
이후에 호출될 인천에서 수원까지 1시간, 수원에서 대전까지 2.5시간, 대전에서 거창까지 2시간이 걸림을 모두 연산할 필요가 없음을 인지하는 것에서 Dynamic Programming은 시작됩니다.
이미 서울의 함수를 호출함으로써 대전에서 거창까지 2시간이 걸린다는 것을 계산한 상태에서 인천의 함수를 호출할 때 대전에서 거창까지 얼마나 걸리는지를 반복해서 계산할 필요가 없다는 것이지요. 그래서 Dynamic Programming은 연산을 하기 전에 다음과 같은 전처리를 하게 됩니다.
int dp[max_n];
int solution(int pos){
if(pos=="거창") return 0;
int& ret = dp[pos];
if(ret!=-1) return ret;
ret=INF;
for(int i=0;i<arr[pos].size();i++){
int there = arr[pos][i].first;
int cost = arr[pos][i].second;
ret=min(ret,solution(there)+cost);
}
return ret;
}
// memset은 #include <cstring>
int main(){
memset(dp,-1,sizeof(dp));
}
먼저 dp라는 Random Access가 O(1)에 가능한 배열을 선언하고 모두 -1이라는 연산 결과에 나올 수 없는 값으로 초기화합니다. 이후에 모든 계산을 하기 전에 각각의 연산 값을 메모이제이션한 뒤 이 연산의 값을 저장하고 있는 배열의 값이 -1이라면 계산을 하고, -1이 아닌 다른 어떠한 값이 들어가 있다면 이전에 계산했던 결과값을 O(1)의 시간에 바로 리턴합니다. 이러한 과정을 통해 이전에 대전에서 거창까지 2시간이 걸림을 배열에 저장했다면 다음 연산에서는 복잡한 계산 과정 없이 O(1)에 전에 계산한 결과값을 바로 가져다 쓰게 되어 중복된 연산이 없어지겠죠.
그렇다면 앞에서 설명해드렸던 Dynamic Programming에 대한 정의가 조금은 더 명확해 지실 겁니다.
각 하위 문제의 해결을 계산한 뒤, 그 해결책을 저장하여 후에 같은 하위 문제가 나왔을 경우 그것을 간단하게 해결할 수 있다. 이러한 방법으로 동적 계획법은 계산 횟수를 줄일 수 있다. 특히 이 방법은 하위 문제의 수가 기하급수적으로 증가할 때 유용하다.
오랜만의 개념 설명이라 혹시 잘못된 코드나 개념 설명은 댓글을 통해 피드백 주시면 감사하겠습니다!.